Leetcode 39- 组合总和
1. 题目描述
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
1 | 示例?1: |
2. 思路
似曾相识的感觉,我第一反应就是递归,比如说找target为7的时候,其实就相当于找target5再在各个list中append一个2,但是递归难免会有重复求解子问题的情况,于是,我又想到了动态规划。
总的来说,就是像如下这样去列举,map中每个value用的是集合,目的是防止重复:1
2
3
4
5
6
7
8
9
10
11input : [2,3,6,7]
res[0] = {}
res[1] = {}
res[2] = res[0]+2 = {[2]}
res[3] = res[0]+3 = {[3]}
res[4] = (res[2]+2) U (res[1]+3) = {[2,2]}
res[5] = (res[3]+2) U (res[2]+3) = {[2,3]}
res[6] = (res[4]+2) U (res[3]+3) U (res[0]+6) = {[2,2,2],[3,3],[6]}
res[7] = (res[5]+2) U (res[4]+3) U (res[1]+6) U (res[0]+7) = {[2,2,3],[7]}
等等
别人的解法
提交动态规划的代码后发现效率不高,只战胜了8%左右的人,于是看了一下别人的题解,第一名是采用递归+剪枝回溯的办法,为了避免重复,最开始也对candidates数组排了个序,因为每个元素又可以重复使用,然后在递归函数中的start参数和保持当前一样就行了。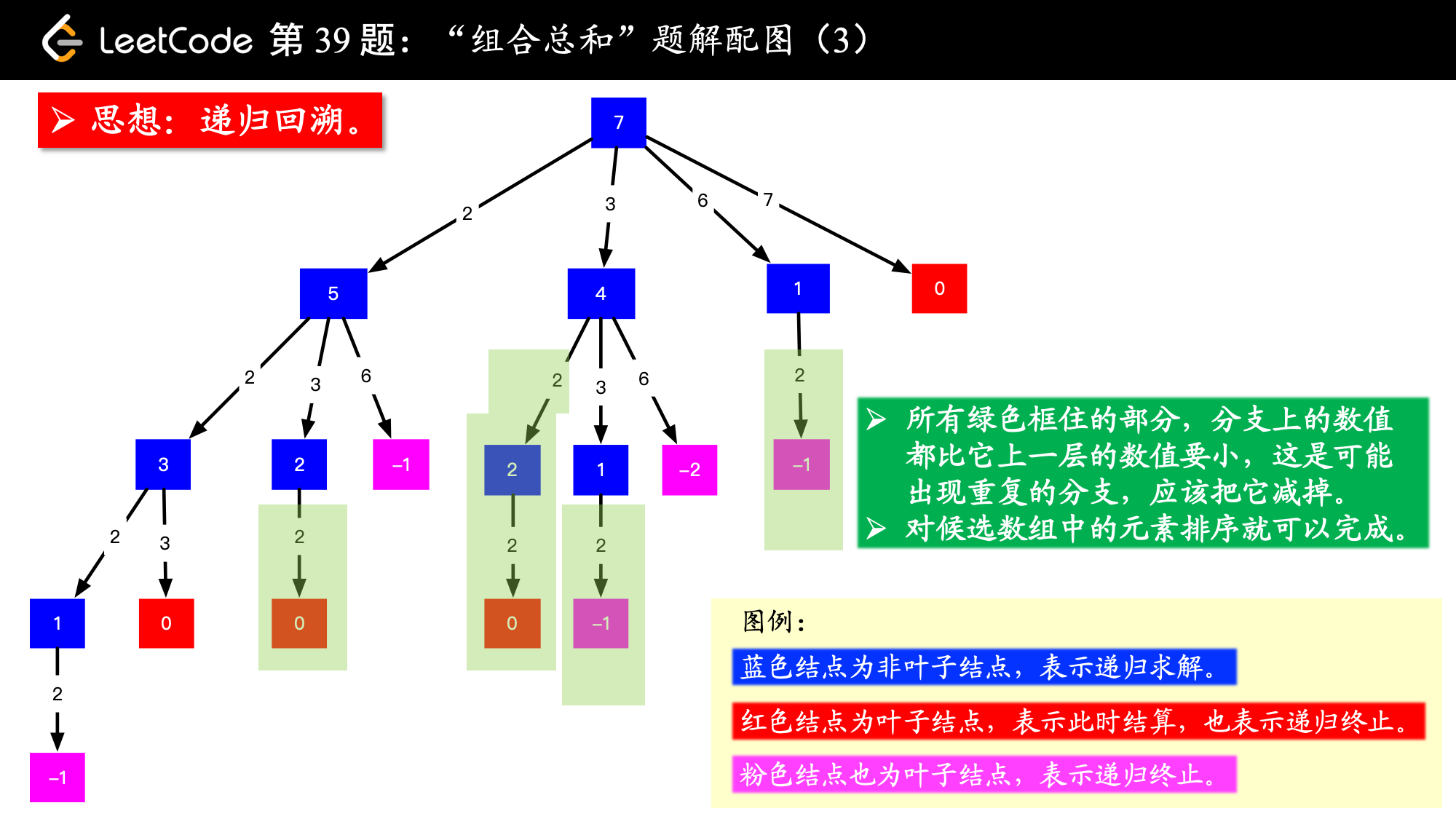
3. 代码
Java 实现
3.1 动态规划
1 | import java.util.*; |
3.2 递归+回溯剪枝
1 | public class Solution { |
4.相似的题目
- Leetcode 40 - 组合总和 ②
这个题和39题几乎一样,不同在于candidates可能有重复元素,且每个元素只能用一次。这里就有一个坑了,假如candidates为[1,2,2,5],现在我要找target=8的时候,如果按照39题的递归的解法,并我们限制每个元素只取一次,也就是每次调用递归函数的时候,begin下标从当前元素的下一个元素开始试探。代码大概张这个样子:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48class Solution {
private int[] candidates;
private int candidates_len;
private List<List<Integer>> res;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
this.candidates = candidates;
this.candidates_len = candidates.length;
this.res = new ArrayList<>();
// 先对candidates排序,防止出现重复
Arrays.sort(candidates);
// 递归求解+剪枝回溯
search(target, 0, new Stack<Integer>());
return this.res;
}
// 从当前下标i对应的值开始试探,直到试探成功或者residue为负数
public void search(int residue, int begin, Stack<Integer> prePath) {
// 试探成功,加入结果集合
if (residue == 0) {
List<Integer> tmpList = new ArrayList<>();
tmpList.addAll(prePath);
res.add(tmpList);
return;
}
// 递归地试探
else {
for (int i = begin; i < candidates_len && candidates[i] <= residue; i++) {
prePath.push(candidates[i]);
// 这里下一次从i+1下标对应的值开始试探,因为题目规定一个值只能用一次
search(residue - candidates[i], i + 1, prePath);
prePath.pop();
}
}
}
public static void main(String[] args) {
int[] cdds = {10, 1, 2, 7, 6, 1, 5};
int target = 8;
Solution s = new Solution();
List<List<Integer>> res = s.combinationSum2(cdds, target);
System.out.println(res);
}
}
然鹅。。。我们会找到两个[1,2,5],虽然说这好像也的确满足每个元素只能用一次,只不过第一个[1,2,5]用的是第一个2,第二个[1,2,5]用的是第二个2,但是还是要注意这种重复情况。所以在下一次递归调用的时候需要判断一下是否有两个一样的元素连在一起。修改好的代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55class Solution {
private int[] candidates;
private int candidates_len;
private List<List<Integer>> res;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
this.candidates = candidates;
this.candidates_len = candidates.length;
this.res = new ArrayList<>();
// 先对candidates排序,防止出现重复
Arrays.sort(candidates);
// 递归求解+剪枝回溯
search(target, 0, new Stack<Integer>());
return this.res;
}
// 从当前下标i对应的值开始试探,直到试探成功或者residue为负数
public void search(int residue, int begin, Stack<Integer> prePath) {
// 试探成功,加入结果集合
if (residue == 0) {
List<Integer> tmpList = new ArrayList<>();
tmpList.addAll(prePath);
res.add(tmpList);
return;
}
// 递归地试探
else {
for (int i = begin; i < candidates_len && candidates[i] <= residue; i++) {
// 这里尤其还要注意一种情况,例如candidates为[1,2,2,5]
// 现在我们要找target=8时,根据我们的算法会生成两个[1,2,5],讲道理,这样也算满足每个元素只用了一次的
// 但是这样还是算重复,于是要考虑删除这种重复。
// 也就是当下一更深层的试探时,如果发现和之前的那个元素值相同,就跳过本轮试探,即:
if (i > begin && candidates[i] == candidates[i - 1])
continue;
prePath.push(candidates[i]);
// 这里下一次从i+1下标对应的值开始试探,因为题目规定一个值只能用一次
search(residue - candidates[i], i + 1, prePath);
prePath.pop();
}
}
}
public static void main(String[] args) {
int[] cdds = {10, 1, 2, 7, 6, 1, 5};
int target = 8;
Solution s = new Solution();
List<List<Integer>> res = s.combinationSum2(cdds, target);
System.out.println(res);
}
}